New Ideas on Hair Breakage: Mending Existing Flaws

Breakage is likely high on any list of hair-related consumer worries. Broken fibers and fray give rise to unsightly split ends, which in sufficient numbers can hinder the ability to grow beautiful, long and flowing hair. Considerable effort has therefore been dedicated to studying the tensile properties of hair and the negative impact of various insults. Previous articles in this column have described this testing process and shown typical results.^1–3 Our historical beliefs as to the causes of hair breakage have accordingly been largely shaped by findings from this approach.

More recently, an alternate mechanical testing technique, fatigue testing, has been changing our perspective on this topic.^{4, 5} First, results suggest considerably more amplified consequences from known harmful treatments; but, at the same time, sizable contributions from hitherto unrecognized factors also become apparent. Contemplation of the reasons for these occurrences leads to a simple and succinct means for visualizing the causes of breakage, while also suggesting strategies for mitigation.

Fatigue Theory

The traditional method for assessing the tendency for hair breakage involves applying a one-time, catastrophic deformation to individual fibers with the subsequent evaluation of a force-to-break. And as described in previous articles, it is common to report a break stress whereby the break force is normalized against fiber dimensions; i.e., stress = force/cross-sectional area. This approach measures the underlying fundamental tensile properties of a fiber but in reality, all materials fail at their weakest point. The presence of any flaw or blemish represents a weakness, which can be propagated by repeated application of minor stimuli such that failure will ultimately occur. By means of illustration, when we hear news stories about bridges failing, it is not because any single vehicle exceeded the bridge’s break threshold. Instead, it is the cumulative effect of many vehicles that gradually propagate minor flaws to failure. In the hair care world, this prompts an analogy to the act of grooming, where each and every brush stroke imparts repeated fatiguing insult to hair fibers.

Flaws in hair fibers can presumably be created by a myriad of different actions. Foremost in our minds, perhaps, are some of the known harmful habits and treatments that are well-documented to compromise the hair protein structure; for example: chemical treatments, heat, UV exposure, etc. Yet flaws seemingly could also be formed by mechanical means where, for example, placing hair in braids or possibly even a ponytail could originate structural chinks. Flaw occurrence will be more likely in longer hair due to an accumulation of wear and tear and a higher statistical likelihood of a flaw being present in a long fiber versus a short one.

New Insights from S-N Plots

To assess how repeated stress can affect fiber breakage, a commercially available instrument can be used that performs single fiber, mechanical fatigue testing.⁶ The device repeatedly applies a user-defined force to single fibers over and over until breakage ultimately occurs. Prior to testing, fiber dimensions are measured with a laser micrometer to allow for the conversion of force into stress units.

Figure 1 shows fatigue results expressed as so-called S-N Plots, where the magnitude of the repeating stress (S) is plotted against the number of cycles of this stress required to cause fiber breakage (N). Figure 1 contains data for both virgin Caucasian hair and that procured from a panelist with shoulder-length hair. Test specimens for the panelist’s hair were taken from the very tips, such that testing occurred on hair with approx. two years of general wear and tear. Despite a relatively high degree of scatter, regression lines for the two data sets are virtually parallel and show the panelist’s hair breaking after about 70% fewer fatiguing strokes, on average.

This conclusion is considerably more worrisome than the approximate 10% decrease in break stress that arises from testing these same samples by the traditional stress-strain approach. As such, it seems our historical reliance on constant extension rate experiments has consistently been producing a sizable under-estimate as to the severity of various treatments on the tendency for hair breakage.

The downward slope of the regression line indicates how faster breakage accompanies higher fatiguing stresses. Conceptually, this appears instinctively correct; but the magnitude of this effect is noteworthy. The logarithmic y-axis indicates the presence of an exponential relationship between the two variables, such that rising fatiguing—grooming—forces result in exponentially faster breakage.

In short, even relatively slight changes in grooming forces can have sizable consequences. To illustrate this point, from Figure 1, a seemingly meager 10% increase in fatiguing forces (i.e., from 0.010–0.011 g/µm²) encountered by virgin Caucasian hair can be calculated to produce an increase in the tendency for fiber breakage comparable to two years' worth of wear and tear, as seen in the panelist’s hair at the same stress.

Effect of Relative Humidity

Another disquieting revelation surfaces when performing hair fatiguing experiments at different relative humidities. As described in previous articles in this series, water is a plasticizer for hair and water content is implicitly tied to the relative humidity of the surrounding environment.^{3, 7} Therefore, hair’s mechanical properties decline with increasing humidity but as noted, amplified effects tend to arise in fatigue experiments.

Conventional mechanical testing on virgin, single-source African hair suggests a dry state break stress that is around 10% lower than virgin Caucasian hair.

Figure 2 shows S-N Plots for virgin Caucasian hair tested at 20%, 60% and 90% relative humidity. Again, the regression lines are essentially parallel and indicate considerable differences in the tendency for breakage. To illustrate, from these regression lines it can be calculated that a repeating 0.012 g/µm2 stress requires approximately 64,000 cycles to cause breakage at 20% RH. Fibers break after around 5,500 cycles at 60% RH while only 250 cycles are necessary at 90% RH.

Once again, we are presented with a non-obvious variable that has a significant effect on hair breakage. Elevated humidity conditions produce an effect comparable to—and possibly greater than—even the most aggressive chemical treatments. This perhaps makes us think about geographical regions where the humidity is often high. However, nearer to home, our own bathrooms—where much hair manipulation takes place—will be especially humid after showering.

So why should these rarely considered factors have such extreme effects on hair breakage?

Flaw Propagation Rates

Returning to fatigue theory, in addition to the presence of flaws being important, so too is their propagation rate. Earlier it was stated how, instinctively, higher fatiguing forces would lead to faster breakage, presumably because flaw propagation rates are exacerbated by a larger stimulus.

Further to this point, as fibers become more pliable, application of an identical force will now result in greater deformation of the sample. This is hypothesized to be the underlying reason for the aforementioned humidity effects. That is, application of a common stress results in greater sample deformation as the relative humidity rises, and so flaws propagate faster under this increased stimulus.

A fundamental scientific precept is that a good hypothesis makes predictions by which it can be tested. To this end, if our hypothesis is true, comparable effects would be expected from any other source of fiber plasticization. Water is able to plasticize hair because it is a small molecule that readily penetrates and interferes with secondary electrostatic bonding within the internal hair protein. Glycerol has similar (albeit lesser) properties but unlike water, it is non-volatile and remains behind after drying. Figure 3 thus shows an S-N Plot of data for hair previously soaked in a 10% glycerol solution. As predicted, a considerably higher tendency for breakage is seen in the treated hair.

Here again, we are faced with another finding that previously would have been considered unusual. Glycerol has long been a staple in hair care formulas, where it is often used to help convey a product’s “moisturization” proposition. Yet, Figure 2 and Figure 3 are strong reinforcers of a previous premise from this series—namely that water is bad for hair.⁷

Effects of Heat on Hair Breakage

Heat also is often a source of plasticization in materials. The high temperatures used in straightening irons—often as high as 230°C or 450°F—are seemingly sufficient to affect the hair protein structure, creating flaws. By our theory, frictional forces in combination with a plasticized state might enhance flaw propagation. Therefore, our evolving theory suggests a potentially sizable tendency for breakage in heat-straightened hair. Figure 4 shows S-N Plots containing data for hair exposed to both 150 and 300 passes with a commercial straightening iron at its maximum heat setting. Substantial effects indeed ensue.

Breakage in African Hair

No article on hair breakage would be complete without some discussion of African hair. This hair type appears especially fragile and “breakage” is widely referenced as one of the primary concerns for individuals with this hair type; so much so that it induces very different habits and practices in the end user. So, does our theory provide explanations?

Conventional mechanical testing on virgin, single-source African hair suggests a dry state break stress that is approximately 10% lower than virgin Caucasian hair. Therefore, this hair type does appear intrinsically weaker but not perhaps to a degree that suggests a need for highly different habits and practices. Figure 5 shows an S-N Plot containing data from fatigue experiments on these same hair types. As seen throughout this article, fatigue testing produces far bigger—and more worrisome—differences. For example, from the regression lines in Figure 5, it can be calculated that a repeating 0.010 g/µm² stress at 60% RH leads to virgin Caucasian hair breakage after approximately 37,000 cycles. Virgin African hair, on the other hand, breaks after only 5,500 such cycles.

On top of this, the highly kinky/curly nature of African hair will result in significantly higher grooming forces. Epps and Wolfram⁸ reported dry state instrumental combing forces for African hair that were around 10 times higher than for Caucasian hair. From calculations based on our regression line, a comparatively meager 50% increase in grooming forces (i.e. from 0.010–0.015 g/µm²) is predicted to induce breakage in African hair after only 25 fatiguing cycles.

Moreover, this still represents virgin African hair. In 2012, Bryant and coworkers⁹ reported an approximate 80% incidence of relaxer usage in this market. These highly caustic treatments substantially compromise the hair structure and produce further considerable weakness.

Heat straightening is also a popular treatment for this hair type. From this short discourse, it quickly becomes evident why breakage in African hair is such a problem.

Known factors such as chemical and heat treatments lead to flaws that are amplified in fatigue testing. But unrecognized factors propogating flaws also must be considered.

It’s All About the Flaws

Our historical perspective of hair breakage has been shaped by traditional stress-strain tensile experiments that provide fundamental information about the underlying protein structure.³ In this way, we recognize how tensile properties can be irreversibly diminished by chemical treatments, which deplete the number of strength-supporting cystine bonds within the hair. Similarly, solvation of secondary electrostatic bonds by water or other such molecules will lower mechanical properties in a reversible manner.

Yet, fatigue experiments lead to profoundly larger differences between samples and suggest profusely higher likelihoods of breakage as the result of known “damage” contributors. Moreover, previously unconsidered factors also raise their heads and can produce effects that outweigh the usual suspects.

Fatigue theory provides a model for understanding these contributions, whereby breakage becomes all about the flaws; that is, the presence of flaws and their propagation rate. Factors we historically considered as contributors to breakage, e.g., chemical treatments, high heat, environmental factors, etc., are those that seemingly lead to the presence of flaws and their amplified effects in fatigue testing experiments has been demonstrated herein.

However, in this type of testing, there is also need for considering as-yet unrecognized factors that influence flaw propagation rates. Accordingly, we come to appreciate the substantial contribution of factors such as the fatigue—grooming—force magnitude, fiber dimensions and fiber stiffness—plasticization—that all arise from the exponential relationship between the magnitude of the fatiguing stimulus and the tendency for breakage (i.e., the S-N Plot). Indeed, our results suggest these contributors seemingly outweigh those of traditional flaw creation insults.

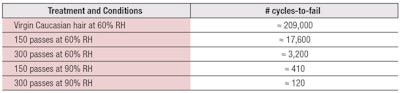
Notwithstanding, these effects are additive where, for example, many insults will weaken the hair structure, adding flaws, and increase grooming forces, speeding flaw propagation. In a similar vein, Table 1 shows average cycles to fail for heat-treated hair (Figure 4) in combination with the effects of elevated humidity. It becomes evident how worrisome levels of breakage can quickly transpire.

At the same time, this learning provides tactics for minimizing hair breakage. Any ability to mend existing flaws seems improbable but strategies for minimizing flaw formation and/or propagation seem more plausible. Earlier it was shown how higher fatiguing forces give rise to exponentially faster hair breakage and so, conversely, lower fatiguing forces could lead to exponentially slower hair breakage. This outcome is readily obtained from the lubrication provided by conventional conditioning products. To this end, repeated grooming experiments^{5, 10} are commonly used as a highly consumer-relevant manifestation of this benefit.

As a measurement scientist working in the hair care industry, it is highly gratifying to be able to recount how a new, properly validated instrumental technique can produce so much new insight in a mature topic.

References

1. TA Evans, Measuring hair strength, part 1: Stress-strain curves, Cosm & Toil 128(8) 590-594 (2013)
2. TA Evans, Beating the damaging effects of heat on hair, Cosm & Toil 130(5) 28-33 (2015)
3. TA Evans, How damaged is Hair? Part 2: Internal damage, Cosm & Toil 132(6) 36-45 (2017)
4. TA Evans, Fatigue testing of hair: A statistical approach to hair breakage, J Cos Sci 60 599-616 (2009)
5. TA Evans, Measuring hair strength, part 2: Fiber breakage, Cosm & Toil 128(12) 854-859 (2013)
6. SB Hornby, NJP Winsey and SP Bucknell, New technique to capture viscoelastic changes in hair induced by mechanical stress, IFSCC Magazine 5 no. 2 (2002)
7. TA Evans, Measuring the water content of hair, Cosm & Toil 129(2) 64-69 (2014)
8. J Epps and LJ Wolfram, Letter to the editor, J Cos Sci 34 213-214 (1963)
9. H Bryant, C Porter and G Yang, Curly hair: Measured differences and contributions to breakage, Int J of Derm 51(1) 8-11 (2012)
10. TA Evans and K Park, A statistical approach to hair breakage. II. Repeated grooming experiments, J Cos Sci 61 439-455 (2010)