Practical Foam Science

Foams seem so simple; put a surfactant in water, mix with air and beautiful bubbles appear instantly. However, almost any change or addition to a foam formula can have multiple effects because foams are complex systems. Life would be easier for the formulator if the science behind foams could be broken down to see how formulation choices could affect specific formulation features—for better or for worse. Because foam science is difficult to understand, the formulator settles for unsatisfactory rules of thumb in hopes that they will solve whatever foam problem is at hand.

The present article explores the key aspects of foam science, including critical micelle concentration (CMC), elasticity, DLVO Theory stability, Ostwald ripening, draining and antifoams. These variables were built into algorithms in a series of free online applications,^a which formulators can access to explore how changes in variables will impact the foam. Most illustrations provided in this article are taken from the online apps; references to the key academic papers used in their development are also provided here.

CMC and Foam

Most formulators know two key parameters for a surfactant: the CMC and the surface tension (γ) at and above the CMC. The energy needed to create a foam is proportional to γ, so more foam is created for less energy with a smaller γ. Typically, foams are generated effectively around the CMC, so a lower CMC means that less surfactant is required.

However, from these two values comes surface concentration of the surfactant (Γ_m), another parameter of importance in understanding foams. Careful scientists can get exact values for Γ_m from the isotherm data obtained by plotting CMC versus concentration. An isotherm can also be approximated from just the CMC and γ,¹ as calculated in Figure 1. The Γ_m value is vital for estimating the elasticity of the foam interface, described next.

Elasticity of Foam

Foam cannot be created without elasticity (E), which is what restores the foam wall upon distortion. Foam based purely on water, for example, has no elastic restoring force and thus breaks up instantly. As one’s intuition suggests, the more elastic the foam wall, the more resistant it is to damage. In addition, a rigid and well-packed foam wall is more resistant to ripening, drainage and antifoams, as will be shown later.

E is basically the change in γ of the wall as the area of the wall increases.² For pure water, there is no change in γ, and no E. If the γ of the wall is low, and increasing the area creates sites with no surfactant, then the change in γ and the E are large. Some readers will know this as the Gibbs or Marangoni effect.

E can be calculated by:

E = 4RT Γ_m² × K² × c/(H (1 + K × c)² + 2Γ_m × K)

Eq. 1

where c is the concentration of surfactant, and K is a constant that depends on the CMC.

Figure 2 shows how the concentration dependence of the elasticity can be calculated for the surfactant in Figure 1. The more surfactant, the higher the elasticity—up to a maximum. Whether the elasticity actually decreases after that is a matter of debate, but according to the laws of physics, it should.

One of the primary ways to raise elasticity in foams is to add small amounts of co-foamers such as lauryl alcohol or myristic acid. They are useless foamers on their own, but once the foam wall has been established by a good foamer (see Figure 3), co-foamers migrate to the wall, “kicking out” the good foamer molecules³ and establishing a rigid wall with high elasticity, 

Disjoining Pressure

Water in foam walls is pulled out by capillary forces, quickly thinning the walls. These capillary forces are relentless, and the walls would collapse to nothing under this “joining” pressure, which ultimately comes down to van der Waals (vdW) attraction. Hence, foams need a “disjoining” pressure to resist collapsing.

There are two forms of disjoining pressure. The least useful form is the steric force from the tails of nonionic surfactants. The walls from steric-stabilized foams are super thin (~ 5 nm) and very easy to break, so nonionics are generally not great foamers. The more useful form of disjoining pressure is charge-induced from ionic surfactants, where the charged heads repel each other across the wall. Thinner walls lead to bigger repulsion.

The theory that describes these forces is called DLVO, named after Derjaguin, Landau, Verwey and Overbeek.⁴ Although it is easy to understand the basics—i.e., “stuff attracts other stuff,” steric inhibition climbs dramatically when tails are touching, and charges repel but are shielded by other charges such as added salt in the formulation—it is difficult to assemble all the required parameters with the right units, as shown in Figure 4.

As the app calculation shows, A_H is the Hamaker constant for the vdW attraction; the surface potential is typically 100 for an ionic and 1-2 for a nonionic; the steric length for a C₁₂ chain is ~ 1 nm; the surface charge is a value between 0 and 1, governing steric stabilization; and the electrolyte concentration and the charges Z1,2 of the ions control the screening of the surface potential. Playing with a DLVO model such as the app is a good way to familiarize with this important concept.

Foam Components

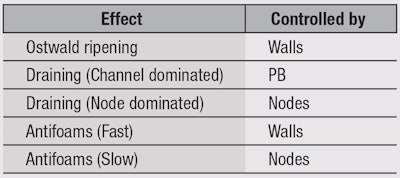
So far, nothing has been mentioned about foams themselves, but to understand the remaining aspects of foam science—Ostwald ripening, draining and antifoams—a review of the main foam components is helpful. Foams consist of a foam wall, plateau borders (PB) and nodes (see Figure 5) and each of these components controls different aspects of foam science (see Table 1). Foam itself is characterized either by the fraction of air (Φ) or fraction of water (ε). Typically, Ostwald theories work in terms of air and draining theories work in terms of water, but because Φ = 1 – ε, it is simple to convert between the two.

Ostwald Ripening

Ostwald ripening causes bubbles to grow larger over time, and because foams are not homogenous, the effects are complex. The pressure inside a bubble of diameter D is proportional to γ/D, so smaller bubbles have larger pressures. Gas inside bubbles with large pressures diffuses into bigger bubbles with smaller pressures—making small bubbles shrink and large bubbles grow. In general, the larger bubbles are more fragile and break more easily; therefore, Ostwald ripening is undesirable for long-lasting foam.

This ripening process is complicated by each foam’s distribution of bubble sizes, the internal pressures of which also depend on how crowded the foam is, so the pressures change as the bubble sizes change. These complexities are calculated by the app, as shown in Figure 6, as well as considered in a paper from the Denkov group.⁵

Describing such a complex model could comprise a whole article itself. The important thing to note is that by playing with the model one variable at a time, it is easy to gain an understanding of which factors are most influential. For example, foams based on CO₂ ripen quickly because the permeation coefficient k is very high, since the Henry constant is high, and because CO₂ is quite soluble in water. In another example, Guinness^b beer leverages these concepts by using N₂ gas with a much lower solubility, Henry constant and permeation to create foam in a glass of their beer that is smaller and lasts much longer.

The other key factor to note in Ostwald ripening is that a rigid surfactant surface greatly reduces permeation of the gas across bubbles. A typical sodium laureth sulfate (SLES) and cocamidopropyl betaine (CAPB) foam has a relatively high permeation, but adding a small percentage of lauryl alcohol or myristic acid makes these molecules go to the surface, “kick out” the SLES and CAPB, and create a rigid, impermeable wall and much longer-lasting foam. As an example, Dawn^c dish soap and Gilette^d shaving foam have surfactants that ripen quickly and slowly, respectively. In the lab, one can go from Dawn-like to Gillette-like just by adding a small amount of myristic acid.

Foam Draining

Foam draining is the loss of water from within the foam. In DLVO theory, water removed from between the walls in a foam is key, but the amount of water in the walls is an irrelevant fraction of the overall water in the foam. Therefore, “draining” of the foam has little to do with activities within the walls. Instead, the action of draining takes place in the PB and/or nodes.

The PB can be considered pipes through which fluid flows—and the laws of such flow are well-known. These laws tell us that if the pipe walls are completely fixed, as in Gillette^d-type foams, then the fluid flow is greatly restricted by interactions with those walls. As the radius (r) of the pipes becomes smaller during drainage, the restriction increases rapidly, as 1/r³. This is classified as channel-dominated foam.

For very fluid surfactant systems, such as Dawn^c-type foams, the walls pose no restriction to flow. In this case, the surfactants in the wall travel with the flow, and the resistance tends to come from the nodes. This is classified as node-dominated foam.

With the app, users choose one type or the other to make calculations; although in reality, systems often contain a bit of both, and the balance between them can change as drainage happens. The many theories of drainage are complex, but the Saint-Jalmes group has provided a framework from which it is possible to create a realistic drainage calculation (see Figure 7).⁶

Again, it would take pages to fully explain what is going on during foam draining, but the main themes are clear. The bubbles are all assumed to have the same given diameter (D) and the foam has a height (H), which is often measured in a foam apparatus. The evolution of the foam height is a key test in any lab that develops shampoos or foam baths. The liquid viscosity, density and surface tension are needed, plus the liquid fraction, ε at the start. The x axis shows the z direction from top (z = 0) to bottom (z = 100 mm). The y axis shows the liquid fraction at regular time intervals.

So after 14 sec, for example, the drainage front has reached 20 mm and the amount of liquid in the foam is the low equilibrium value at the top, rising steadily to the original value at 20 mm. After 21 sec, the front has moved another 10 mm. In other words, the foam is draining with a steady velocity (at the drainage front) of 1.52 mm/sec. For this node-dominated flow, the front velocity (v_f) is given by the following, where L is the PB length ~ D/3:

v_f = 0.002ρgL²√ε/µ

Eq. 2

The take-home message is: for a nice, wet foam that does not drain too quickly, small bubbles are needed, and doubling the size quadruples the drainage speed. For high viscosity, add some glycerol.

In the example in Figure 7, the difference in drainage between a rigid and fluid surfactant interface is small—the drainage line for the foam reaches the bottom of the foam column after 62 sec instead of 68 sec in the node-dominated calculation described above. In reality, foams do not choose between ripening or draining, though, they do both at the same time. These two idealized models should therefore be coupled together to give a more realistic model. This is doable (see the Saint-Jalmes paper⁶), as the apps show, but these models do not represent real foam floating in the bath or piled atop someone’s hair. Rather, they are provided here to clarify the science of the individual elements so that the practical formulator can think through the implications of a formulation change on each of the key aspects of a foam.

Antifoams

Sometimes foam is to be avoided, such as during the manufacture of products that contain surfactants for reasons such as “coatability.” At other times, a stable foam undisrupted by small amounts of oils is desired, e.g., when a formulation is washing dirt away from the user’s skin and hair. So, it is important for foam scientists to understand the mechanism of antifoams as well.

An antifoam is an oily drop, hydrophobic particle or mixture that enters the foam wall and causes the wall to disrupt or “de-wet” around the oily drop or particle. Any explanation of antifoams will mention three parameters: entry (E), bridging (B) and spreading (S) coefficients.⁷ They depend on the interfacial energies between air/water (γ_AW), oil/water (γ_OW) and oil/air (γ_OA). If either E or B is “wrong,” then an antifoam cannot work. This has largely been verified, although note that there is ongoing debate about S. For years it was thought that if all coefficients were “right,” then the antifoam must work but to everyone’s frustration, there have been many examples where such an antifoam did nothing. These equations and a small calculator are provided in the apps. As shown in Figure 8, all three values highlighted in red means that this oil should be a good antifoam, in this context. The oil, however, might not work as an antifoam, as explained in key ideas from the Denkov group.⁶

The first key idea is that “fast” antifoams, i.e., those that provide instant destruction, work directly at the foam wall. As the foam is being created, if an antifoam drop/particle with the right E, B and S attributes arrives at the wall and is large enough to poke through it, the antifoam will do its job quickly and effectively. However, many antifoams work in “slow” mode, meaning the antifoam seems to have no effect for many seconds until the foam suddenly collapses. This happens when particles are sitting between the walls but are swept out as the walls drain, ending up in the PB and then in the nodes.

Since the PB and nodes are much larger than the thickness of the foam walls, the chances are small that the particles can puncture them—until the liquid has drained sufficiently from the nodes and the particles are then relatively large enough to poke through and destroy the foam. This is why some antifoams have no effect for many seconds or minutes. However, even the slow mode must consider one extra factor—the ability to overcome the entry barrier produced by the surfactant layer.

The entry barrier is real, and it can be readily measured using the Film Trapping Technique (FTT),⁷ which applies pressure to an air/water film that traps some antifoam drops/particles between the film and glass. While viewing the glass through a microscope, one increases the pressure on the film until the particles break through. This critical pressure (P_c) is the missing factor in these antifoam studies. The rigid foam layers discussed above with high elasticity, slow Ostwald ripening and slower “channel-dominated” drainage, i.e., foams that are stable to all the usual destructive forces, also have a high P_c, making it difficult for antifoam particles to penetrate and cause destruction. Ideally researchers interested in antifoams should have the capability for measuring P_c. However, it seems that the FTT is not easy in practice, so the world awaits a more user-friendly technique.

The formulator may wonder if oils, particles or mixtures are the best defoamers but the answer is a little more abstract than they may want. The best defoamer has to be the right size and shape, i.e., sharp particles have a lower P_c than round ones. It must also have the right hydrophobicity, and it must be readily added to the foaming solution. These last two factors are contradictory. Highly hydrophobic particles might be great defoamers but if they do not disperse, or if they disperse by attracting surfactant to wrap around them and render them hydrophilic, they are useless. Less hydrophobic particles are easier to disperse but if they are insufficiently hydrophobic, they will fail by the E, B and S criteria.

In short, there are no easy answers on antifoams, but the formulator should be knowledgeable of E, B and S to improve their understanding of fast and slow antifoams. That knowledge, combined with an awareness of P_c, will ultimately improve the chances of successfully formulating an antifoam.

Finally, formulators can develop cleansing foams that account for the resistance of antifoaming action from oils in the hair or skin, or from the hydrophobic conditioners added to foaming formulations. A “wet” foam that drains slowly and is based on a rigid surfactant wall, perhaps created by some small percent of additive, will have little trouble resisting the antifoaming action of such oils.

The Magic of Mixes

If a strong foam is desired, the standard composition is SLES/CAPB with some optional lauryl alcohol or myristic acid. Or, nonionics may be added to an SLES formulation. Also, some ionics may be added to a relatively poorly foaming alkyl polyglucoside (APG), to give it a bit more foam. Such mixes can exist because a good foam is a balance of properties; a good and fast foamer such as SLES, combined with a poor foamer such as myristic acid, which provides a rigid and elastic interface, can be ideal.

CAPB is itself a good foamer, but SLES/CAPB is able to pack more tightly. Nonionics dilute the head-to-head repulsions that cause ionics to have a relatively high CMC, so they can give stronger packing at lower overall surfactant concentration. APGs cannot give strong foam walls because their disjoining pressure is too low, so an ionic addition such as a glutamate surfactant can give thicker foam walls, which are more resistant to the antifoaming action of oils.

To arrive at a novel, superior foaming mix, formulators can use trial and error with gut instinct but preferably, they should know what to measure and have the tools to measure it. In particular, gaining a direct understanding of elasticity and P_c would seem a fruitful way to optimize mixtures for a strong interfacial wall with all the benefits that brings.

The ability to measure surface properties dynamically—i.e., the speed at which surfactants get to the surface—also addresses an area not explicitly covered in the apps. As mentioned previously, SLES is a fast foamer because it gets to the interface quickly. Many key co-foamers are useless on their own because they are far too slow. Polymeric surfactants can have outstanding foam properties given enough time, but they are large molecules that get to the interface slowly. They generally need fast, less efficient co-foamers to produce a foam in the first place. Getting these dynamics right is clearly crucial to good formulations.

Hasten Slowly

Any good foam lab has bubble or Ross-Miles testers with the ability to measure maximum foam height and height changes as a function of time—to get some sort of measure of foaming capability. Foams are usually complex mixtures, making the trial and error approach to development very time-intensive. While investing in systems to measure dynamic surface tension, elasticity and P_c is a “hasten slowly” approach to foam development, it takes time to learn how to get the best out of these measurements. It may slow development in the short term, but it will pay off in the long term as trial and error gives way to intelligent optimization based on good science.

Author’s note: The Practical Foams app series contains in-depth explanations of all the above and includes discussions on making foams and foam rheology. It is a work in progress, so by the time readers visit the site, the apps will have further refinements and extra insights. The author positively welcomes feedback from experts (improving the models) and non-experts (improving the relevance to real formulations) so foam formulation becomes less of a mystery and more of a routine branch of formulation science.

Acknowledgements: The author is grateful for the help and support from some of the world’s top foam groups: the Denkov group in Sofia, Bulgaria; the Saint-Jalmes group in Rennes, France; and the Stubenrauch group in Stuttgart, Germany. Errors or inaccuracies in the implementation and explanation of the science are the author’s fault.

References

1. M Rosen, Surfactants and Interfacial Phenomena, 3rd edn, John Wiley (2004)
2. L Wang and RH Yoon, Effects of surface forces and film elasticity on froth stability, Int J Min Proc 85, 101–110 (2008)
3. ND Denkov, et al, The role of surfactant type and bubble surface mobility in foam rheology, Soft Matter 5 3389–3408 (2009)
4. www.sciencedirect.com/science/article/pii/S0927776599000296 (Accessed Sep 15, 2014)
5. Slavka Tcholakova et al, Control of Ostwald ripening by using surfactants with high surface modulus, Langmuir 27 14807–14819 (2011)
6. A Saint-Jalmes, Physical chemistry in foam drainage and coarsening, Soft Matter 2 836–849 (2006)
7. ND Denkov and KG Marinova, Antifoam effects of solid particles, oil drops and oil-solid compounds in aqueous foams, ch 10 in Colloidal Particles at Liquid Interfaces, BP Binks and TS Horozov, eds, Cambridge University Press (2006) pp 383-444