Editor’s note: Light impacts the way we view the world and each other. It interacts with skin and hair, reflecting and refracting to impart various effects—benign and otherwise. It also influences the products you develop, both in their package and on your consumers. This primer on light reviews the fundamentals of photophysics, to enlighten cosmetic scientists with the underlying behavior and makeup of this natural force.
Log in to view the full article
Editor’s note: Light impacts the way we view the world and each other. It interacts with skin and hair, reflecting and refracting to impart various effects—benign and otherwise. It also influences the products you develop, both in their package and on your consumers. This primer on light reviews the fundamentals of photophysics, to enlighten cosmetic scientists with the underlying behavior and makeup of this natural force.
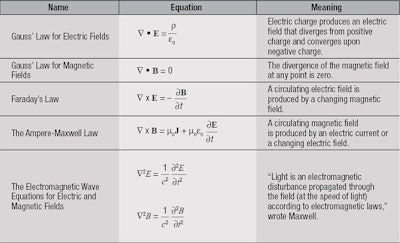
In the late 1600s, Sir Isaac Newton suggested that light is composed of a dense stream of extremely tiny particles called corpuscles. His contemporary, Christiaan Huygens, thought light was made of waves that vibrate up and down, perpendicular to their direction of travel. In the mid 1800s, James Clerk Maxwell developed a series of mathematical equations, known now as Maxwell’s Equations, which led inescapably to the conclusion that the electric and magnetic forces are waves that propagate at the speed of light through space, and that light must be a similar electromagnetic disturbance in a medium he called the luminiferous aether.
Maxwell’s equations were so successful at unifying electricity, magnetism and light and predicting their behavior that they became—and remain—the foundation of modern electrical technologies and communications (see Table 1). So, the matter seemed to have been settled: light was composed of waves.
To the physicists of the time, this made sense. For example, when traveling through a continuous medium, the intensity of a wave spreads out across its wavefront and decreases with the inverse square of its distance. Light measured from a point source that radiates in all directions will have one quarter its intensity at two meters than it does at one meter.
Light exhibits other wave-like characteristics including diffraction and two-slit interference. This further implies that, like other wave phenomena, the light wave’s energy is a function of its amplitude, i.e., the vertical distance between its peak and its trough.
The UV Catastrophe and Black Bodies
But around 1900, it was recognized that there was a problem with this wave view of light; one so big that it was called a catastrophe—specifically the UV catastrophe. The problem was that Maxwell’s description of light as waves could not account for the complete spectrum of colors or frequencies that metal bars and other objects emitted when heated; and especially the ones they don’t emit. The following explains.
Most everybody is familiar with the terms red hot and white hot. These terms are rooted in the experience that dense, solid objects glow with colors that change as temperature increases. First they glow red, then orange, then yellow, then white, then blue. Such objects behave as “black bodies,” which are idealized physical objects that perfectly absorb all electromagnetic radiation and radiate thermal energy incandescently. By the late 1800s, the temperature-dependent spectrum of black body radiation was well-known.
A closed chamber with perfectly reflective walls is a particular type of black body. According to classical (pre-quantum) theory, the total energy of the emitted radiation at a given temperature should be equally divided among the frequencies emitted. The energy of each emitted frequency of light and the total emitted energy was thought to obey the relationship: E = T/λ4, where T is the temperature and λ is the wavelength of the light. Unfortunately, this implies that at higher frequencies (shorter wavelengths), energy becomes unlimited. This was a ridiculous result, and one that did not fit the observation that radiation below short-wave UV is not emitted at all.
Planck’s Constant and Einstein’s Rebuttal of Maxwell
Numerous attempts to find a mathematical equation to fit the black body observations failed until Planck’s Constant was included in the calculations. Planck’s function imposed a limit on the frequencies of light that could be emitted at higher temperatures, which averted the UV catastrophe. Applying Planck’s Constant to the equation perfectly predicted the actual spectrum of black body radiation.
But the real and lasting importance of Planck’s contribution was its repudiation of the idea that electromagnetic energy is absorbed and emitted continuously. Instead, as Planck’s function implied, it is absorbed and emitted in multiples of a basic constant, 6.626 × 10-34 J∙s (Joules times seconds), now called Planck’s Constant.
Albert Einstein took Planck’s idea that energy could only be absorbed and emitted in discrete amounts and extended it to light itself. In 1905, Albert Einstein published no less than five papers that changed physics forever. In one of them, he explained a much-studied phenomenon called the photoelectric effect. This term was originally used to describe the ejection of electrons from a metal surface when it is exposed to radiation of a sufficiently short wavelength.
Einstein explained this phenomenon by relating the energy required to liberate a single electron from the metal surface to the energy contained in a single unit of light, which he termed a light quantum and which is now called a photon. For his discovery, Einstein was belatedly awarded the 1921 Nobel Prize for Physics. This principle that light of the right energy can liberate electrons from the surface of selected materials finds application today in uses as diverse as the solar cells that power watches and homes, to the doors that open automatically in stores and hotels.
Einstein’s new explanation of the photoelectric effect contradicted Maxwell’s theory that energy in light is spread out in a wave. Further, Einstein believed that energy in electromagnetic radiation, including light, is not related to its intensity, as Maxwell’s theory suggested. Rather, it is related to its frequency, through the equation: E = hν, where h is Planck’s Constant and the Greek letter nu, ν, is the radiation’s frequency.
Photoelectric Effect Explained
Given Einstein’s new equation, the photoelectric effect becomes more easily understandable, as follows.
If, in a given metal, the electrons are bound with a certain energy—call it the threshold energy—and if one photon interacts with one electron, then a photon with less than the threshold energy will have no effect while a photon exceeding the threshold will cause the ejection of the electron. Taken a step further, the ejected electron will acquire additional kinetic energy equal to the difference between the photon’s energy and the threshold. Thus, radiation of a higher intensity will liberate more electrons but only if its component photons exceed the threshold energy.
An elegant consequence of Einstein’s prediction is that, for any metal, when the kinetic energy of the liberated electrons are plotted on a graph against the frequency of the radiation used, the resulting slope (rise over run) is always equal to Planck’s Constant.
Perhaps you’ve noticed that Einstein’s idea of the photon still retains one important link to Maxwell’s theories: the photon’s energy is a function of its frequency, and frequency is a wave-like property. It wasn’t until 18 years later, in 1923, that the wave-like and particle-like properties of energy and matter were formally related by the French physicist, Louis de Broglie, whose work you will learn more about later.
The work and ideas of Planck, Einstein and de Broglie lead to the inescapable conclusion that the subatomic world is quantized. This means that in the world of atoms, molecules, electrons and photons, everything happens in little steps called quanta, where a single quantum is the smallest unit of energy. As we learned above, the quantum of linear motion is known as Planck’s Constant (h) and is equal to 6.626 × 10-34 J seconds. The quantum of angular momentum (rotational motion) is called h-bar (ħ) and equal to h divided by 2π (π = 3.14159)
Photons carry electromagnetic force and because they have wave-like properties, their energy is expressed in terms of their wavelength, frequency and wavenumber. As Einstein proposed, the energy (E) of a photon is equal to its frequency (ν) times Planck’s Constant (h), or E = hν. Here, ν is expressed in Hertz (Hz), which is the number of oscillations per second. Scientists and engineers generally prefer to express frequency in radians per second, called angular frequency and given the symbol ω such that E = hν = ħω.
A photon’s frequency (ν) times its wavelength (λ) is usually expressed in nm, which is equal to the speed of light, or c. Thus: νλ = c and ν = c/λ. Therefore, another way of expressing the energy in a photon is: E = hc/λ. The wavenumber ( ν ) is simply the reciprocal of the wavelength or 1/λ, and is in units of cm-1 or reciprocal centimeters. The wavenumber is a convenient metric because like frequency, it is directly proportional to energy. In other words, as energy increases, the wavenumber also increases—unlike wavelength, which decreases. For this reason, the results of many spectroscopic measurements including near-infrared spectroscopy (NIR) are often reported in wavenumbers.
To convert wavelength to wavenumber, first express the wavelength in cm, then divide into 1 as follows: 400 nm = 4 × 10-5 cm; therefore ν = 1/(4 × 10-5 cm) = 25,000 cm-1. For a 300-nm photon, the calculation is 300 nm = 3 × 10-5 cm; therefore ν = 1/(3 × 10-5 cm) = 33,333 cm-1. As you can see, the wavenumber increases in magnitude with energy.
De Broglie on Waves and Momentum
Now, on to the contribution of Louis de Broglie. Based on our everyday experiences, it’s hard to imagine the objects around us as anything other than what we see: solid objects that may or may not be in motion at a given moment. But modern physics tells us that all objects in motion have wavelike properties, although they are imperceptible to our human senses.
In 1924, De Broglie related an object’s wave behavior to its momentum as λ = h/p, where p = mv. This means the wavelength of an object (λ) is equal to Planck’s constant (h) divided by its momentum (p); and p is the product of the object’s mass (m) times its velocity (v). The larger the object’s mass and/or velocity, the shorter the wavelength. This is why the wavelengths of everyday objects are not perceptible to us—they are too short to see.
Take, for example, a golf ball in flight. With a mass of 45.93 g (0.04593 kg), a well-struck golf ball moves at a velocity of approximately 70 meters per second (m/s) (about 156 miles per hour). Its momentum is therefore 0.04593 × 70 = 3.2151 kg × m/s. Planck’s Constant, 6.626 × 10-34 J sec, divided by 3.2151 yields a wavelength of 2.06 × 10-34 meters, or 2.04 × 10-25 nm. That’s 25 orders of magnitude smaller than one billionth of a meter. No wonder we can’t see it!
Now let’s do the same calculation for an electron. We will not know the velocity of the electron but under a given set of experimental conditions, we will know its kinetic energy. So we’ll use a slightly different form of the de Broglie wavelength equation. In this form, the momentum (p) is equal to the square root of twice the electron’s mass (m) times its kinetic energy (T), written: p = √2mT.
The mass of the electron is 9.1 x 10-31 kg. Accelerated across a potential of one volt, its kinetic energy, T, is 1 eV (electron volts) or 1.6 × 10-19 J. Thus, p = √(2*9.1 × 10-31)(1.6 × 10-19) = 5.4 × 10-25. So, with De Broglie relating the electron’s wave behavior to its momentum as λ = h/p, the calculation is (6.626 × 10-34) /(5.4 × 10-25) = 1.2 × 10-9 or about 1.2 nm.
Many molecules are one-half to a few nm in diameter, so the electron’s wave is on the order of molecular size. The electrons in chemical bonds have somewhat higher kinetic energies, on the order of 10 eV, so their de Broglie wavelengths are typically 0.4 nm. This is roughly the size of the chemical bonds themselves.
This leads to an important conclusion: the wave properties of large objects—here, “large” means larger than a molecule—are insignificant even if they actually exist. This is not so with subatomic particles such as electrons. Their wave properties are key to understanding their actions and interactions with other subatomic particles, including photons.
Wave-particle Duality
It fell to the pioneers of quantum mechanics, i.e., Werner Heinsenberg, Erwin Schrödinger, Max Born, Niels Bohr, Wolfgang Paulie, Paul Dirac, John von Neumann and others, to give mathematical form to Einstein’s photons and to de Broglie’s waves. In their interpretation, which applies equally to subatomic particles including electrons, a photon of light behaves as a wave most of the time. Only at the moment of interaction with a resonant electron does a photon’s wave—or more precisely, its wave function—“collapse” into its particle form and disappear as the photon’s energy is transferred entirely to the electron. Such behavior is known as wave-particle duality. In other words, the photon lives its “life” as a wave but ends its life as a bullet.
Conclusions
Quantum mechanics continues to this day as the guiding paradigm of atomic and molecular physics, and underlies fields as diverse as quantum chemistry, nuclear physics and solid state physics. Its practical applications include computers, satellite and mobile communications, GPS and flat screen televisions; in short, much of what makes modern life modern. Of course, that includes the cosmetically related fields of photoprotection and all the many ways that we, as cosmetic scientists, seek through makeup and other means to change the appearance of skin. For we physicists and engineers, an understanding of light unquestionably “illuminates” our work.
References
- D Fleisch, A Student’s Guide to Maxwell’s Equations, Cambridge University Press, Cambridge, UK (2008)
- PA Cox, Introduction to Quantum Theory and Atomic Structure, Oxford University Press, New York (1996)
- L Lederman and D Teresi, The God Particle: If the universe is the answer, what is the question? Houghton Mifflin, New York (1993)
- www.slac.stanford.edu/pubs/beamline/30/2/30-2-carson.pdf
- www-history.mcs.st-andrews.ac.uk/Extras/Planck_on_light.html
- A Einstein and L Infeld, The Evolution of Physics, Cambridge University Press, London (1938)
Market Intelligence
The global sun care market is among the smallest personal care segments, according to Euromonitor figures. However, it is forecast to grow 6.4% to about $10 billion by 2018, with results roughly split between emerging and mature markets.
Source: GCI (www.GCImagazine.com)
