Oil being a non-polar liquid and water being highly polar, initially it was thought the two could never mix.1 With time, this concept has undergone many changes. At the interface of these two phases always exists an energy barrier, hence the mixing of the two immiscible phases can occur only if that barrier is crossed.
Initially, in the 1920s, researchers tried simple stirring, which resulted in temporary mixing but after stirring ceased, the system went back to its separated state. The addition of surfactants allowed the phases to easily mix and remain as such since surfactants significantly reduce the interfacial free energy or tension, helping to disperse one phase into the other. These types of dispersive systems have high stability when prepared properly, and are typically composed of water in oil, or oil in water; in some cases, silicone. Such systems came to be known as emulsions.
Theoretically, the interfacial free energy between two phases can be given as:
∆G = −γo/w ∆A Eq. 1
where the oil/water interfacial tension is represented by γo/w and ∆A is the increase in surface area due to emulsification.
Emulsions are typically thick blends characterized by large, statistically distributed particle sizes.2-4 With the help of short chain alkanols, Schulman and Hoar5 transformed these emulsions into those with much smaller-sized particles, which came to be known as microemulsions. Microemulsions were formulated as early as 1928 and known by various terms, e.g., micro-dispersions, swollen micelles, transparent suspensions, etc.; it was not until 1958 that microemulsions were named as such.
Microemulsion Components, Categories and Behavior
Microemulsions typically consist of four main components: surfactant (emulsifiers); co-surfactant; oil, either as a dispersed phase or dispersion medium; and water, also as a dispersed phase or dispersion medium. They are thermodynamically stable, homogeneous, optically isotropic solutions. Winsor classified microemulsions as four types.5-8
Winsor Type I: Here, two phases are considered: the lower microemulsion phase and the upper excess oil. Both phases are in equilibrium.
Winsor Type II: This type also consists of two phases: the upper microemulsion phase and the lower excess water. Both phases are, again, in equilibrium with each other.
Winsor Type III: Here, the middle microemulsion phase is in equilibrium with both the upper excess oil and lower excess water.
Winsor Type IV: This type is characterized by a single phase: the surfactant, water and oil are all mixed homogeneously.
Microemulsions are formed by three basic approaches: the mixed film theory, as described by Schulman and Prince;9 solubilization theory, as suggested by Shinoda, Friberg et al.;10, 11 and thermodynamic treatment, as described by Ruckenstein, Overbeek and Isralsachicvili et al.12-14
Mixed film theory: This theory assumes the interface as a two-faced wall, with a water side and oil side. The film tension is given by:
γ = γo/w − π Eq. 2
where γo/w is the interfacial tension and π is the spreading pressure of the mixed film. The resulting value depends on the type and concentration of the amphiphiles as well as the amount of oil that can reach the interface. It increases as the interfacial area increases and the net γ tends to become zero, resulting in the dispersion.
Solubilization theory: This theory was introduced by Gilberg et al. and Shinoda.15, 16 Here, the microemulsion is referred to as a swollen micelle system in that the oil and water are solubilized inside the micelles. These authors studied phase diagrams along with the solubilization of hydrocarbons and water in nonionic surfactants.
Thermodynamic theory: Proposed by Ruckenstein et al. and Overbeek, for this theory, Ruckenstein suggested a three-step energy bar:
- The interfacial free energy, ∆Ga
- The interaction energy between droplets, ∆Gb and
- The energy of dispersion of the droplets in the continuous medium.
Consider the droplet radius R and the constant volume fraction of the droplet as Ø. Thus, the total energy is:
∆G(r) = ∆Ga + ∆Gb - T∆S Eq. 3
Overbeek took a slightly different approach:
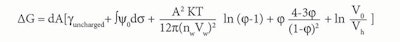
Eq. 4
Where dA is the change in interfacial area; γuncharged is the interfacial tension in the absence of a double layer; and ∫ψ0dσ is the electrical contribution to the interfacial tension resulting from the formation of a double layer. The third term is the osmotic contribution due to the mixing of microemulsion droplets with the continuous medium. Finally, Vh is the molar volume.
Microemulsions often are confused with critical solutions. However, there is distinct difference. In a critical solution, the partially miscible liquids mix completely at two different temperatures.17-23 Unlike microemulsions, the solvents in a critical solution are molecularly dispersed and chemically bonded to form stable complexes. Also, in a critical solution, the mixing is spontaneous whereas microemulsions require an emulsifier.
Various categories of microemulsions exist, including polar oil, polymer oil, biological and others. Kunieda and Moulik reported many biological microemulsions,24, 25 whose biomembranes, comprising proteins, carbohydrates, lipids, etc., can be added to a system to make bio-compatible as well as bio-relevant microemulsions.
For biological microemulsions, emulsifiers such as dioctyl sodium sulfosuccinatea, sodium deoxycholate and octylphenol ethoxylateb have been used. Along with these, gelatin, bovine, cholesterol and other additives can be used, or oils including hydrocarbons, eucalyptus oil, clove oil and cinnamic alcohol.
Microemulsions in the Literature
Much work on microemulsions has been reported in the literature. For examples, the phase behavior of polyoxyethylene hydrogenated castor oil was studied by Kunieda et al.26 Shinoda and Kaneko26 assessed lecithin-based microemulsions and looked at the compatibility of biological amphiphiles and hydrocarbons. Others examined the microstructure of microemulsions and assessed the effect of alcohols and temperature on them.27-31
Backlund et al.32 inspected the microemulsion of soybean lecithin and ethanol, with respect to ethanol concentration and phase behavior. Cavallaro et al. inspected the structural details of water/lecithin and cyclohexane microemulsions.33-37 FTIR spectroscopies of microemulsions also have been reported, as have laminated sponges38 for the buccal delivery of carvedilol microemulsion systems.
Numerous scientists have reported on nonaqueous microemulsions.39-43 Flectcher and Rico described a system of glycerol/heptane/dioctyl sodium sulfosuccinatea and formamide/butanol/cyclohexane/cetyl trimethylammonium bromide (CTAB), respectively.44, 45 Several quaternary and ternary systems also have been reported.46, 47 Finally, Dorfler et al. studied various types of quaternary systems such as aliphatic alcohols/dodecane/SDS/water, in some cases replacing the water component.48
One of the most important parameters for creating the desired emulsion or microemulsion is choosing the right emulsifier for a given oil.
Emulsifier Choice, HLB and HLD
One of the most important parameters for creating the desired emulsion or microemulsion is the right emulsifier choice for a given oil. This mainly is decided by the proportion of hydrophobic to hydrophilic parts of surfactants. This essentially depicts the partitioning value of a surfactant in between the oil and aqueous media. When the hydrophilic-lipophilic balance (HLB) value of the surfactant matches the required HLB of the oil, a stable microemulsion is obtained.
This is an empirical property and signifies surface activity. It is an age-old concept; hence, many formulas exist to calculate the HLB. The HLB scale ranges from 0 to 20 and governs many properties. “Good” emulsifying agents are normally found in the range of 13 to 17.
Griffin HLB: In 1954, Griffin devised an equation to find the HLB as follows.
HLB = 20 Mh/M Eq. 5
where Mh is the molecular mass of the hydrophilic portion and M is the molecular mass of the whole molecule.
Davies HLB: In, 1957 Davies took it further with the equation:
HLB = 7 + m × Hh - n × Hl Eq. 6
where m is the number of hydrophilic groups in the molecule; Hh is the hydrophilic value; n is the number of lipophilic groups in the molecule and Hl is the lipophilic value.
O’Lenick 3D HLB: Although the HLB system is a fair indicator for emulsifier choice, is not always accurate. For instance, in the case of silicone surfactants, the HLB concept is misleading because silicones are mostly organic or inorganic hybrids, so they cannot be placed in conventional hydrophobic or hydrophilic categories. In answer, O’Lenick et al. developed a three-dimensional HLB concept.49, 50 For this extended HLB concept, all the three components of the molecule that are soluble in silicone, oil or water are considered.
Abbott HLD: In another approach, Abbot51-53 came up with the concept of HLD, i.e., the difference of hydrophobicity and hydrophilicity. HLD simplified and also eased the formulator’s job of choosing a suitable emulsifier, to some extent. An HLD near zero indicates optimum conditions, whereas large values indicate poor formulations and small positive or negative values indicate perfect oil/water or water/oil microemulsions. Scientists further combined this with the concept of net average curvature to create an even more balanced approach:
Curvature = 1/R = HLD/l Eq. 7
where R is ≥ the radius of the micro globules in either o/w or w/o microemulsions, and l is a constant parameter 1.2 times the length of the surfactant tail. Research is ongoing to create a more compact scientific basis for making microemulsion formulations. Attempts have even been made to create a database to assists the formulators.
(Continued to Part II)